Paradox

A paradoxical notice

PLEASE IGNORE THIS NOTICE

Some proofs

Happiness or a ham sandwich?

Which is better, eternal happiness or a ham sandwich? It would appear that eternal happiness is better, but this is really not so! After all, nothing is better than eternal happiness, and a ham sandwich is certainly better than nothing. Therefore a ham sandwich is better than eternal happiness.

The liar paradox

The following version is the version which we will refer to as the liar paradox. Consider the statement in the following box:

THIS SENTENCE IS FALSE

Is that sentence true or false? If it is false then it is true, and if it is true then it is false...

The following version of the liar paradox was first proposed by the English mathematician P E B Jourdain in 1913. It is sometimes referred to as "Jourdain's Card Paradox". We have a card on one side of which is written:

(1) THE SENTENCE ON THE OTHER SIDE OF THIS CARD IS TRUE

Then you turn the card over, and on the other side is written:

(2) THE SENTENCE ON THE OTHER SIDE OF THIS CARD IS FALSE

... Another popular version of the liar paradox is given by the following three sentences written on a card.

(1) THIS SENTENCE CONTAINS FIVE WORDS

(2) THIS SENTENCE CONTAINS EIGHT WORDS

(3) EXACTLY ONE SENTENCE ON THIS CARD IS TRUE

Mobius band W

A Mobius band has just one side and just one edge.

Penrose triangle W

Necker cube (Freemish crate) W

Ames room W

Missing square paradox W

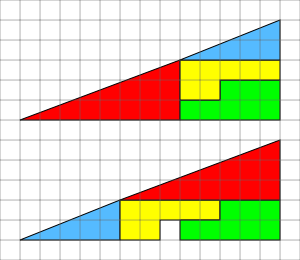
Arithmetic and algebraic paradoxes

Proving that 2 = 1

Here is the version offered by Augustus De Morgan: Let x = 1. Then x² = x. So x² - 1 = x -1. Dividing both sides by x -1, we conclude that x + 1 = 1; that is, since x = 1, 2 = 1.

Quine, p.5

Assume that

a = b. (1)

Multiplying both sides by a,

a² = ab. (2)

Subtracting b² from both sides,

a² - b² = ab - b² . (3)

Factorizing both sides,

(a + b)(a - b) = b(a - b). (4)

Dividing both sides by (a - b),

a + b = b. (5)

If now we take a = b = 1, we conclude that 2 = 1. Or we can subtract b from both sides and conclude that a, which can be taken as any number, must be equal to zero. Or we can substitute b for a and conclude that any number is double itself. Our result can thus be interpreted in a number of ways, all equally ridiculous.

Northrop, p. 85

The paradox arises from a disguised breach of the arithmetical prohibition on division by zero, occurring at (5): since a = b, dividing both sides by (a - b) is dividing by zero, which renders the equation meaningless. As Northrop goes on to show, the same trick can be used to prove, e.g., that any two unequal numbers are equal, or that all positive whole numbers are equal.

Here is another example:

Proving that 3 + 2 = 0

Assume A + B = C, and assume A = 3 and B = 2.

Multiply both sides of the equation A + B = C by (A + B).

We obtain A² + 2AB + B² = C(A + B)

Rearranging the terms we have

A² + AB - AC = - AB - B² + BC

Factoring out (A + B - C), we have

A(A + B - C) = - B(A + B - C)

Dividing both sides by (A + B - C), that is, dividing by zero, we get A = - B, or A + B = 0, which is evidently absurd.

Kasner & Newman, p. 183

Proving that n = n + 1

(a) (n + 1)² = n² + 2n + 1

(b) (n + 1)² - (2n + 1) = n²

(c) Subtracting n(2n + 1) from both sides and factoring, we have

(d) (n + 1)² - (n + 1)(2n + 1) = n² - n(2n +1)

(e) Adding ¼(2n + 1)² to both sides of (d) yields

(n + 1)² - (n + 1)(2n + 1) + ¼(2n + 1)² = n² - n(2n + 1) + ¼(2n + 1)²

This may be written:

(f) [(n + 1) - ½(2n + 1)]² = [(n - ½(2n + 1)]²

Taking square roots of both sides,

(g) n + 1 - ½(2n + 1) = n - ½(2n + 1)

and, therefore,

(h) n = n + 1

Kasner & Newman, p. 184

The trick here is to ignore the fact that there are two square roots for any positive number, one positive and one negative: the square roots of 4 are 2 and -2, which can be written as ±2. So (g) should properly read:

±(n + 1 - ½(2n + 1)) = ±(n - ½(2n + 1))